시험기간이다..
수업시간에 배운 자료구조를 다시 복습해봐야겠다.
[자료구조]LinearSearch.c 와 BinarySearch.c 의 코드와 시간복잡도
LinearSearch.c
우선 순차탐색 LinearSearch.c 의 핵심코드는 아래와 같다
for (i = 0; i < len; i++)
{
if (arr[i] == target)
return i;
}
target 값이 배열의 요소로 있다면 배열의 인덱스 값은 반환시켜 주는 것이다.
이때, 시간 복잡도는 최악의 경우(worst case)를 고려하여 짜는데,
LinearSearch 의 경우,
"데이터의 수가 n개 일때, 최악의 경우에 해당하는 연산횟수는 n이다."
따라서, T(n) = n 이다.
BinarySearch.c
우선 이진탐색 BinarySearch.c 의 핵심코드는 아래와 같다
while (first <= last)
{
mid = (first + last) / 2;
if (target == arr[mid])
return mid;
else
{
if (target <= arr[mid])
last = mid-1;
else
first = mid+1;
}
}first와 last 를 이용하여 mid를 갱신하고 mid가 인덱스로 들어가는 target 값을 찾는 방식이다.
이때의 경우도 마찬가지로, 시간 복잡도는 최악의 경우(worst case)를 고려하여 짜는데,
BinarySearch 의 경우,
결과만 놓고 보면,
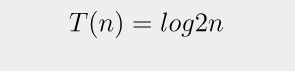
왜 그렇게 되는지 살펴보면 아래 이미지와 같다.

최종적으로 LinearSearch 의 시간복잡도는 O(n).
BinarySearch의 시간복잡도는 O(log n) 이다. 어떤 것이 더 효율적일까?
이를 비교하기 위한 코드를 아래에 첨부하였다.
#include <stdio.h>
#include "BinaryHead.h"
int main(void)
{
int arr1[500] = { 0, };
int arr2[5000] = { 0, };
int arr3[50000] = { 0, };
int idx;
idx = BSearch(arr1, sizeof(arr1) / sizeof(int), 1);
ShowInfo(idx);
idx = BSearch(arr2, sizeof(arr2) / sizeof(int), 1);
ShowInfo(idx);
idx = BSearch(arr3, sizeof(arr3) / sizeof(int), 1);
ShowInfo(idx);
return 0;
}
#pragma once
int BSearch(int arr[], int len, int target)
{
int first = 0;
int last = len - 1;
int mid;
int opCount = 0; //비교 연산의 횟수 기록
while (first <= last)
{
mid = (first + last) / 2;
if (target == arr[mid])
return mid;
else
{
if (target <= arr[mid])
last = mid - 1;
else
first = mid + 1;
}
opCount++; //비교 연산 횟수 1 증가
}
printf("비교연산횟수 : %d\n", opCount); //탐색실팻시 연산 횟수 출력
return -1;
}
void ShowInfo(int idx)
{
if (idx == -1)
printf("탐색 실패\n");
else
printf("타겟 저장 인덱스 : %d\n", idx);
}이진 탐색의 연산횟수가 훨씬 더 적다는 것을 알 수 있다.

'c' 카테고리의 다른 글
| [c언어/열혈 c프로그래밍] p.83 문제 04-2 <데이터 표현의 이해> (0) | 2023.08.03 |
|---|---|
| [c언어/열혈 c프로그래밍] p.82 문제 04-1 <진법의 이해> (0) | 2023.08.03 |
| [c/c++] 구조체로 학생 성적 처리 (0) | 2023.03.05 |
| [c/c++] 문자열 정의 : 1)포인터 2)배열 (0) | 2023.03.04 |
| [git 파일 올리기 에러] See the 'Note about fast-forwards' in 'git push --help' for details. (깃 에러/ 깃 커밋 에러) (0) | 2023.03.01 |


